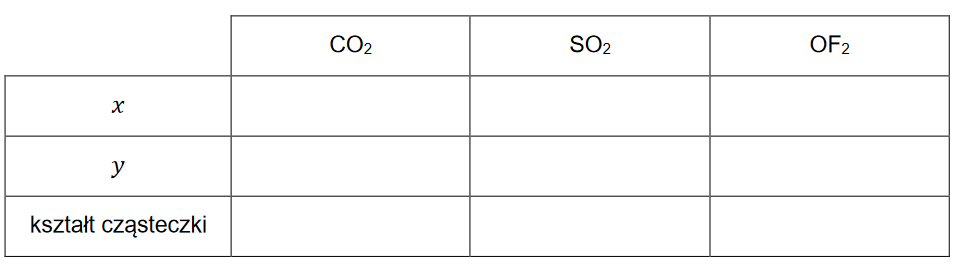
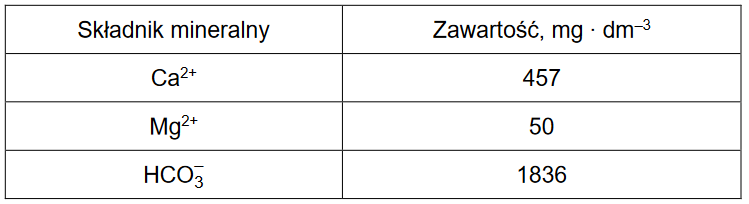
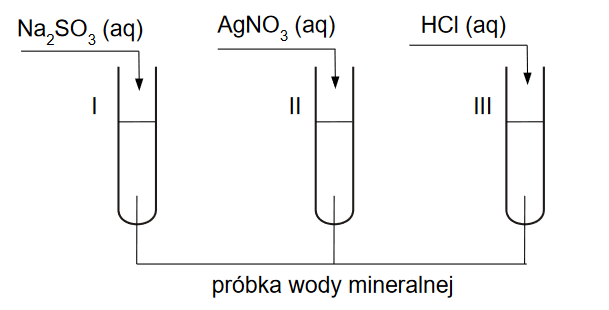
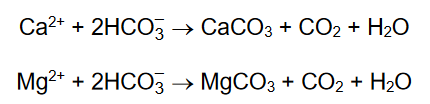Budowa atomu
EGZAMIN MATURALNY Z CHEMII POZIOM ROZSZERZONY MARZEC 2022
Na podstawie budowy atomów pierwiastków należących do grup 1.–2. oraz 13.–17. drugiego okresu układu okresowego uzupełnij poniższe zdanie. W wyznaczone miejsca wpisz symbol albo nazwę odpowiedniego pierwiastka.
Spośród pierwiastków drugiego okresu:
• najmniejszy ładunek jądra ma atom:
• najmniejszy promień atomowy ma atom:
• najmniejszą wartość pierwszej energii jonizacji ma atom:
budowa atomu
INFORMATOR o egzaminie maturalnym z chemii 22/23
Wybierz parę pierwiastków, których atomy w stanie podstawowym mają różne liczby niesparowanych elektronów. Zaznacz poprawną odpowiedź.
A. krzem i tytan
B. siarka i tytan
C. krzem i żelazo
D. siarka i nikiel
Budowa atomu – wiązania chemiczne
INFORMATOR o egzaminie maturalnym z chemii 22/23
Tlenek krzemu (SiO 2), nazywany potocznie krzemionką, jest bardzo rozpowszechniony
w przyrodzie. Czysta krzemionka występuje w postaci krystalicznej, np. jako minerał kwarc.
Poniżej przedstawiono zdjęcie kryształów kwarcu oraz model jego struktury krystalicznej.
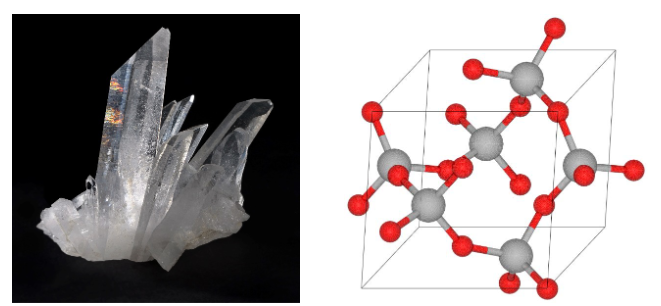
Dokończ zdanie. Zaznacz odpowiedź spośród A–D i jej uzasadnienie spośród 1.–4.
Kwarc można zaliczyć do kryształów

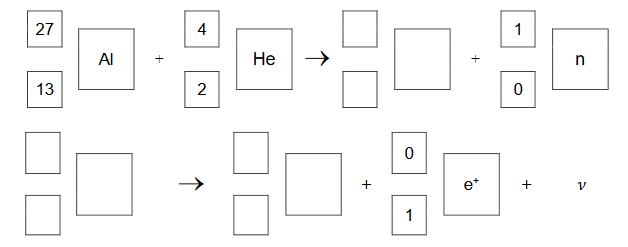
bombardowanie folii aluminiowej cząstkami alfa
INFORMATOR o egzaminie maturalnym z chemii 22/23
Podczas bombardowania folii aluminiowej cząstkami alfa zachodzą procesy jądrowe z równoczesną emisją pozytonów i neutronów. Stwierdzono, że przemiana jest dwuetapowa: w pierwszej reakcji jądrowej powstają niestabilne jądro i neutron, a potem następuje rozpad β+ tego niestabilnego jądra, któremu towarzyszy emisja neutrino ν.
Napisz równania opisanej przemiany jądrowej. Uzupełnij poniższe schematy.
Promieniotwórczość ciężkojonowa
INFORMATOR o egzaminie maturalnym z chemii 22/23
Promieniotwórczość ciężkojonowa to szczególny i rzadki rodzaj promieniotwórczości. Polega na emisji z ciężkiego jądra atomowego jąder atomów lekkiego pierwiastka. Równania takich rozpadów promieniotwórczych zapisuje się zgodnie z zasadami zachowania: ładunku elektrycznego jąder oraz liczby nukleonów.
Napisz równanie rozpadu jądra promieniotwórczego izotopu Ac 89 223 , z którego jest emitowane jądro izotopu węgla zawierające 8 neutronów.
Atom siarki i jego związki
INFORMATOR o egzaminie maturalnym z chemii 22/23
Atom siarki tworzy z atomami fluoru m.in. cząsteczki o wzorze SF2 i SF6.
1. Narysuj wzór elektronowy cząsteczki SF2 – zaznacz kreskami wspólne pary elektronowe oraz wolne pary elektronowe atomów siarki i fluoru. Określ kształt cząsteczki (liniowa, kątowa, tetraedryczna).
Wzór elektronowy:
Kształt cząsteczki:
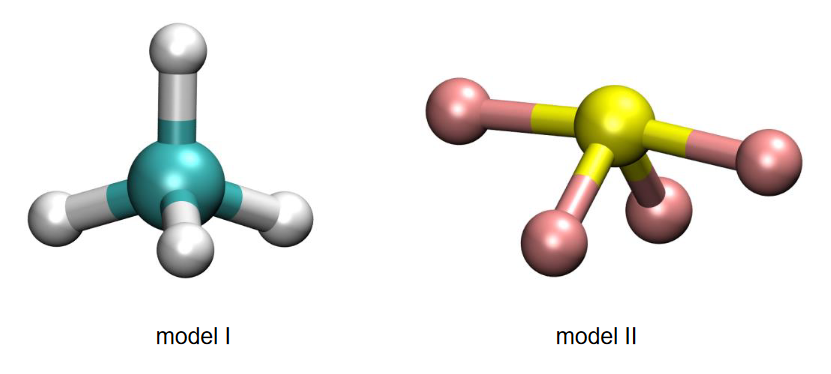
2. Poniżej zamieszczono model ilustrujący kształt cząsteczki SF6.

Wykaż na podstawie teorii VSEPR (odpychanie par elektronowych powłoki walencyjnej), że przedstawiony model jest poprawną ilustracją kształtu cząsteczki SF6.
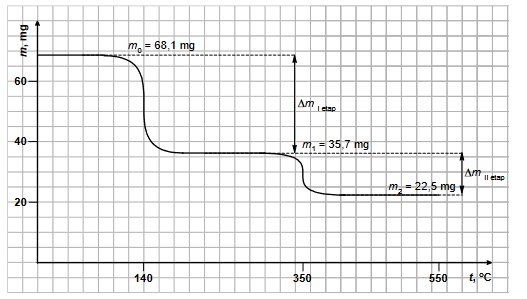
Obserwacja zmian energii wewnętrznej układu w wyniku przemiany chemicznej
INFORMATOR o egzaminie maturalnym z chemii 22/23
Przeprowadzono doświadczenie, którego celem była obserwacja zmian energii wewnętrznej badanego układu w wyniku przemiany chemicznej. W procesie przeprowadzonym w warunkach izotermiczno-izobarycznych wprowadzono do cylindra gazowy tlen oraz sproszkowane żelazo i zamknięto ten cylinder ruchomym tłokiem. Schemat doświadczenia przedstawiono na poniższym rysunku.
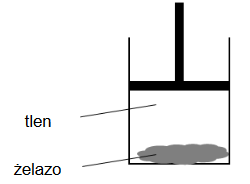
W warunkach doświadczenia reakcja zachodziła z niewielką szybkością. Ścianki cylindra umożliwiały wymianę ciepła z otoczeniem.
Uzupełnij poniższe zdania. Wybierz i zaznacz jedną odpowiedź spośród podanych w każdym nawiasie.
W wyniku przebiegu opisanego procesu tlen się zużywa, a tłok przesuwa się (w dół / w górę), wykonując pracę nad układem. Przemianie żelaza w tlenek żelaza(III) towarzyszyło odprowadzenie ciepła do otoczenia, co oznacza, że ta reakcja jest procesem (endoenergetycznym / egzoenergetycznym).
Wykres zmian stężeń reagentów w czasie
INFORMATOR o egzaminie maturalnym z chemii 22/23
Do reaktora o stałej pojemności, z którego usunięto powietrze, wprowadzono próbkę gazowego związku A i zainicjowano reakcję. W zamkniętym reaktorze ustaliła się równowaga opisana równaniem:
A (g) ⇄ 2B (g)
Mierzono stężenie związku A w czasie trwania reakcji. Tę zależność przedstawiono na poniższym wykresie:
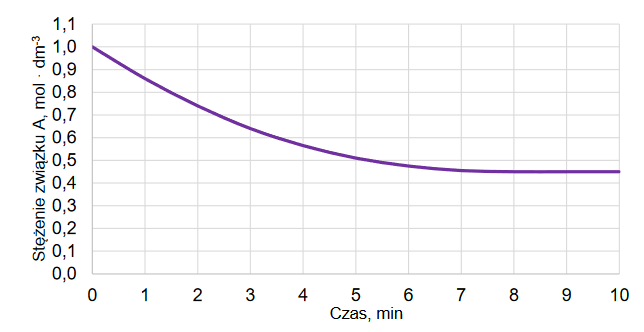
Z poniższych wykresów wybierz ten, który jest ilustracją zależność stężenia związku B od czasu trwania reakcji. Zaznacz wykres A, B, C albo D i uzasadnij swój wybór.
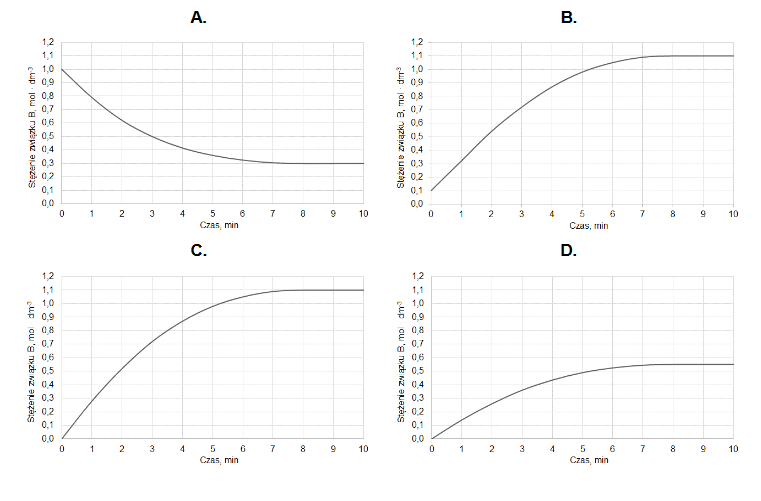
Uzasadnienie:
Tlenki metali – wzór empiryczny i rzeczywisty związku chemicznego
INFORMATOR o egzaminie maturalnym z chemii 22/23
Dwa tlenki metali, oznaczone umownie wzorami A₂O i XO₃, reagują ze sobą w stosunku molowym 1:1. Produktem reakcji jest jonowy związek Z, w którym masowa zawartość procentowa pierwiastka A wynosi 40,2%, natomiast dla pierwiastka X ta wielkość jest równa 26,8%.
1. Na podstawie obliczeń ustal symbole pierwiastków A i X.
2. Zaznacz numer zdjęcia, na którym przedstawiono związek Z.

Działanie kwasu solnego na węglan wapnia – doświadczenie
INFORMATOR o egzaminie maturalnym z chemii 22/23
Uczniowie wykonywali doświadczenie, podczas którego działali kwasem solnym na węglan wapnia, w zestawie umożliwiającym pochłanianie wydzielającego się CO2 w roztworze KOH. Naczynie z tym roztworem miało być zważone przed doświadczeniem i po jego zakończeniu.
Reakcje wydzielania i pochłaniania CO2 opisują równania:
CaCO3 + 2HCl → CaCl2 + H2O + CO2
CO2 + 2KOH → K2CO3 + H2O
Węglan wapnia był stosowany w nadmiarze, natomiast kwas solny miał nieznane stężenie, ale mógł zostać dokładnie odmierzony. Na podstawie jego objętości oraz przyrostu masy naczynia z KOH, uczniowie mieli oszacować stężenie roztworu HCl. Swoje pomiary zapisali w poniższej tabeli:

Okazało się, że jeden z uczniów błędnie zmierzył lub błędnie zapisał przyrost masy.
Oblicz stężenie molowe badanego roztworu na podstawie wyników ucznia I i ucznia II. Wskaż ucznia, który poprawnie wykonał doświadczenie. Odpowiedź uzasadnij.